Muốn giải được bài tập đạo hàm tốt thì trước tiên bạn phải xem lại công thức đạo hàm đã được học ở bài trước. Dựa vào lý thuyết đó bạn sẽ dễ dàng luyện được kĩ năng giải bài tập đạo hàm hiệu quả.

Bài tập đạo hàm có lời giải
Bài tập 1: Hãy tính đạo hàm cơ bản sau $y = {x^3} – 3{x^2} + 2x + 1$
Giải
Sử dụng công thức đạo hàm ta có: $y’ = \left( { – {x^3} + 3x + 1} \right)’ = 3{x^2} – 6x + 2$
Bài tập 2: Cho hàm số có chứa căn như sau $y = \frac{{2x + 1}}{{x – 3}}$. Hãy tính đạo hàm
Giải
Vận dụng công thức đạo hàm của hàm hợp: $y’ = \frac{{(2x + 1)'(x – 3) – (x – 3)'(2x + 1)}}{{{{(x – 3)}^2}}} = \frac{{ – 7}}{{{{(x – 3)}^2}}}$
Bài tập 3: Cho một hàm số $f(x) = \sqrt {{x^2} – x + 1} + \sqrt {{x^2} + x + 1} $. Hãy tính đạo hàm
Giải
Sử dụng công thức đạo hàm của hàm hợp ta giải như sau
Ta có: $f'(x) = \frac{{2x – 1}}{{2\sqrt {{x^2} – x + 1} }} + \frac{{2x + 1}}{{2\sqrt {{x^2} + x + 1} }}$
Suy ra $f'(x) = 0 \Leftrightarrow \left( {1 – 2x} \right)\sqrt {{x^2} + x + 1} = \left( {1 + 2x} \right)\sqrt {{x^2} – x + 1} $
$\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} (1 – 2x)(1 + 2x) \ge 0\\ {(1 – 2x)^2}\left[ {{{\left( {x + \frac{1}{2}} \right)}^2} + \frac{3}{4}} \right] = {\left( {1 + 2x} \right)^2}\left[ {{{\left( {x – \frac{1}{2}} \right)}^2} + \frac{3}{4}} \right] \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} – \frac{1}{2} \le x \le \frac{1}{2}\\ {(1 – 2x)^2} = {(1 + 2x)^2} \end{array} \right. \Leftrightarrow x = 0 \end{array}$
Bài tập 4: Cho hàm số $y = {\sin ^2}3x$. Hãy tính đạo hàm
Giải
Đây là hàm số lượng giác nên ta vận dụng công thức đạo hàm của hàm lượng giác suy ra
$y’ = 3\sin 6x$
Bài tập 5: Cho hàm số lượng giác $y = \sqrt {3{{\tan }^2}x + \cot 2x} $. Hãy vận dụng công thức đạo hàm lượng giác để tính đạo hàm
Giải
Vận dụng công thức đạo hàm lượng giác và hàm hợp:
Ta có: $y’ = \frac{{3\tan x(1 + {{\tan }^2}x) – (1 + {{\cot }^2}2x)}}{{\sqrt {3{{\tan }^2}x + \cot 2x} }}$
Bài tập đạo hàm phân theo dạng
Dạng 1: Tính đạo hàm bằng định nghĩa
Bài tập 1: Cho hàm số f(x) = x2 + 2x, có Δx là số gia của đối số tại x = 1, Δy là số gia tương ứng của hàm số. Khi đó Δy bằng:
A. (Δx)2 + 2Δx
B. (Δx)2 + 4Δx
C. (Δx)2 + 2Δx – 3
D. 3
Giải
Đáp án: B
Δy = f(1 + Δx) – f(1) = (1 + Δx)2 + 2(1 + Δx) – (1 + 2) = (Δx)2 + 4Δx
Đáp án B
Bài tập 2: Đạo hàm của các hàm số sau tại các điểm đã cho: f(x) = x2 + 1 tại x = 1?
A. 1/2
B. 1
C. 0
D. 2
Giải
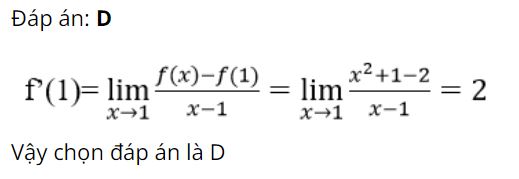
Bài tập 3: Đạo hàm của các hàm số sau tại các điểm đã cho: f(x) = 2x3 + 1 tại x = 2?
A. 10
B. 24
C. 22
D. 42
Giải
Đáp án: B
Ta có
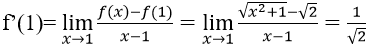
Vậy chọn đáp án là B
Dạng 2: Tính đạo hàm bằng công thức
Bài tập 4: Đạo hàm của hàm số y = (2x4 – 3x2 – 5x)(x2 – 7x) bằng biểu thức nào dưới đây?
A. (8x3 – 6x – 5)(2x – 7)
B. (8x3 – 6x – 5)(x2 – 7x) – (2x4 – 3x2 – 5x)(2x – 7)
C. (8x3 – 6x – 5)(x2 – 7x)+(2x4 – 3x2 – 5x)(2x – 7)
D. (8x3 – 6x – 5) + (2x – 7)
Giải
Đáp án: C
Áp dụng công thưc đạo hàm hàm hơp (uv)’= u’v + uv’ ta có:
y’ = (8x3 – 6x – 5)(x2 – 7x) + (2x4 – 3x2 – 5x)(2x – 7)
Chọn đáp án là C
Bài tập 5: Đạo hàm của hàm số f(t) = a3t4 – 2at2 + 3t – 5a bằng biểu thức nào sau đây?
A. 4a3t3 – 4at + 3
B. 3a2t4 – 2t2 – 5
C. 12a2t3 – 4at – 2
D. 4a3t3 – 4at – 5
Giải
Đáp án: A
f'(t) = 4a3t3 – 4at + 3
Chọn đáp án là A
Bài tập 6: Đạo hàm của hàm số f(x) = a3 – 3at2 – 5t3(với a là hằng số) bằng biểu thức nào sau đây?
A. 3a2 – 6at – 15t2
B. 3a2 – 3t2
C. -6at – 15t2
D. 3a2 – 3t2 – 6at – 15t2
Giải
Đáp án: C
f(t) = a3 – 3at2 – 5t3
f'(t) = -6at – 15t2
Chọn đáp án là C
Dạng 3: Tính đạo hàm của hàm số lượng giác
Bài tập 7: Đạo hàm của hàm số:
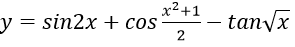 bằng biểu thức nào sau đây?
bằng biểu thức nào sau đây?
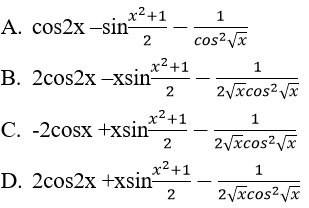
Giải
Đáp án: B
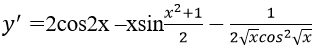
Đáp án B
Bài tập 8: Đạo hàm của hàm số:
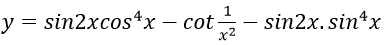 bằng biểu thức nào sau đây?
bằng biểu thức nào sau đây?
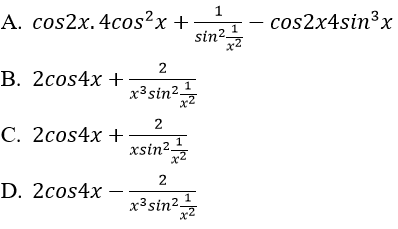
Giải
Đáp án: D
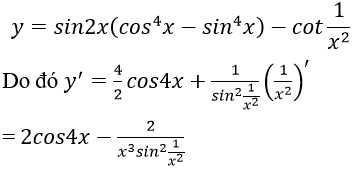
Bài tập 9: Đạo hàm của hàm số y = 6(sin4x + cos4x) – 4(sin6x + cos6x) bằng biểu thức nào sau đây?
A. 24(sin3x + cos3x) – 24(sin5x + cos5x)
B. 24(sin3x – cos3x) – 24(sin5x + cos5x)
C. 2
D. 0
Giải
Đáp án: D
y’= 6(sin2x + cos2x)2 – 12sin2xcos2x – 4(sin2x + cos2x)2 + 12sin2xcos2x(sin2x + cos2x) = 2
Dạng 4: Đạo hàm của hàm hợp
Bài tập 10. Tính đạo hàm của hàm số: y= ( 5x+ 2)10.
A . 10( 5x+2)9
B. 50( 5x+2)9
C. 5( 5x+2)9
D.(5x+2)9
Giải
Đạo hàm của hàm số đã cho là: y’=10.(5x+2)9.( 5x+2)’=50(5x+2)9
Chọn B.
Bài tập 11. Đạo hàm của hàm số y = f(x)= ( 1- 3x2,)5 là:
A. -30x.(1-3x2 )4
B. -10x.(1-3x2 )4
C. 30(1-3x2 )4
D. -3x.(1-3x2 )4
Giải
Đặt u (x)= 1- 3×2 suy ra u (x)=( 1-3x2 )’=(1)’-3(x2 )’= -6x
Với u= 1-3×2 thì y= u5 suy ra y‘ (u)=5.u4=5.(1-3x2)4
Áp dụng công thức đạo hàm của hàm hợp ta có :
y‘ (x)= 5.(1-3x2 )4.(-6x)= -30x.(1-3x2 )4
Chọn A.
Bài tập 12. Tính đạo hàm của hàm số : y= ( x3+ x2 -1)2 ( 2x+1)2
A. y’= ( x3+ x2-1)( 3x2+2x).(2x+1)2+(x3+ x2-1)2.( 8x+4)
B. y’= 2( x3+ x2-1)( 3x2+2x).(2x+1)2+(x3+ x2-1)2.( 8x+4)
C. y’= ( x3+ x2-1)( 3x2+2x).(2x+1)2+(x3+ x2-1)2.( 4x+4)
D. y’= 2( x3+ x2-1)( 3x2+2x).(2x+1)2-(x3+ x2-1)2.( 8x+4)
Giải
áp dụng công thức đạo hàm của của hàm hợp và đạo hàm của một tích ta có :
y’=[( x3+ x2-1) ]2‘.(2x+1)2+(x3+ x2-1)2.[(2x+1)2]’
Hay y’=2( x3+ x2-1)( x3+ x2-1)’.(2x+1)2+
(x3+ x2-1)2.2( 2x+1).(2x+1)’
⇔ y’= 2( x3+ x2-1)( 3x2+2x).(2x+1)2+(x3+ x2-1)2.2( 2x+1).2
⇔ y’= 2( x3+ x2-1)( 3x2+2x).(2x+1)2+(x3+ x2-1)2.( 8x+4)
Dạng 5: Đạo hàm và các bài toán giải phương trình, bất phương trình
Bài tập 13. Cho hàm số y= 2x3 – 6x2+ 2000. Phương trình y’= 0 có mấy nghiệm?
A. 0
B. 1
C. 2
D. 3
Giải
+ Ta có đạo hàm: y’=6x2-12x
+ Để y’=0 thì 6x2-12x=0
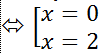
Vậy phương trình y’= 0 có hai nghiệm.
Chọn C.
Bài tập 14. Cho hàm số y= x4+ 2x3 – k.x2+ x- 10. Tìm k để phương trình y’=1 có một nghiệm là x= 1?
A. k= 5
B. k= -5
C. k= 2
D. k= – 3
Giải
+ Ta có đạo hàm: y’= 4x3+ 6x2 – 2kx+ 1.
+ Để y’= 1 thì 4x3+ 6x2 – 2kx+ 1 = 1
⇔ 4x3+ 6x2 – 2kx = 0. (*)
Do phương trình y’= 1 có một nghiệm là x= 1 nên phương trình (*) có một nghiệm x= 1. Suy ra: 4.13 + 6.12 – 2.k.1= 0 ⇔ 10- 2k = 0
⇔ k= 5.
Chọn A.
Bài tập 15. Cho hàm số y= 2mx – mx3. Với những giá trị nào của m để x= -1 là nghiệm của bất phương trình y'<1?
A. m > – 1
B. m < 1
C.m= 1
D. m < – 1
Giải
Ta có đạo hàm: y’= 2m- 3mx2
Bất phương trình y’ <1 khi 2m-3mx2 <1
Do x= -1 là nghiệm của bât phương trình nên ta có: 2m- 3m.(-1)2 < 1
⇔ – m < <1 hay m >- 1.
Chọn A.
Dạng 6: Tính đạo hàm tại 1 điểm
Bài tập 16. Cho hàm số y= x3+ 2x2 – 2x+ 10. Tính đạo hàm của hàm số tại x= 1
A. 5
B. – 2
C. 7
D. 10
Giải
Đạo hàm của hàm số đã cho là : y’= 3x2 +4x- 2
⇒ Đạo hàm của hàm số tại điểm x=1 là y’ ( 1)= 3. 12+ 4.1- 2= 5
Chọn A.
Bài tập 17. Cho hàm số y= 16√x+2x- x2. Tính đạo hàm của hàm số tại x= 4.
A. – 1
B. – 2
C. 0
D. 2
Giải
Tại các điểm x > 0 thì hàm số đã cho có đạo hàm và y’= 8/√x+2-2x
⇒ Đạo hàm của hàm số đã cho tại x= 4 là : y’ ( 4)= 8/√4+2-2.4= -2
Chọn B.
Bài tập 18. Cho hàm số y= ( 2x+ x2)2. Tính đạo hàm của hàm số tại x= – 1?
A. 0
B. 2
C. – 2
D .4
Giải
Hàm số đã cho xác định với mọi x.
Đạo hàm của hàm số đã cho là:
y’=2( 2x+ x2 )( 2x+ x2 )’ = 2( 2x+ x2 )( 2+2x)
⇒Đạo hàm của hàm số tại x= -1 là y’( – 1) = 0.
Chọn A.
Dạng 7: Đạo hàm và bài toán giải phương trình, bất phương trình lượng giác
Bài tập 19. Cho hàm số: y= sinx+ cosx. Tìm nghiệm của phương trình y’=0
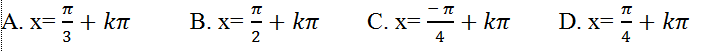
Giải
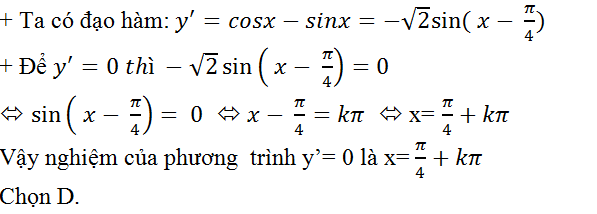
Bài tập 20. Cho hàm số: y= tanx+ cot x. Giải phương trình y’=0

Giải
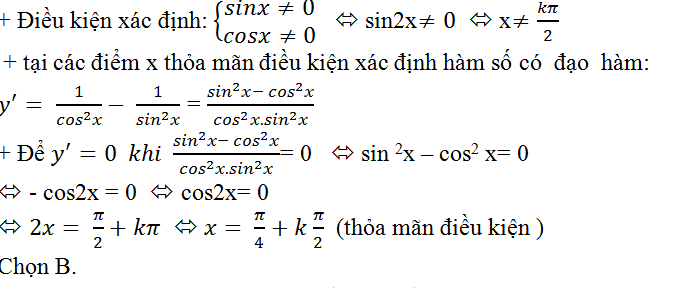
Bài tập 21. Cho hàm số y=x3+ 3x+ sin3 x. Giải bất phương trình y’ ≥0

Giải
Ta có đạo hàm: y’=3x2+ 3+ 3sin2x. cosx
Với mọi x ta có; cosx ≥ – 1 ⇒ 3sin2 x.cosx ≥ – 3.sin2 x
⇒ 3+ 3sin2x.cosx ≥ 3- 3.sin2 x ⇔ 3+ 3sin2x.cosx ≥ 3.cos2x ( 1)
Lại có 3x2 ≥0 ∀ x (2)
Từ( 1) và ( 2) vế cộng vế ta có:
y’=3x2+ 3+ 3sin2x. cosx ≥3x2+3cos2 x ≥0 với mọi x.
Vậy với mọi x ta luôn có: y’ ≥0
Chọn C.
Bạn nên xem thêm bài tập đạo hàm lượng giác nâng cao để hiểu thêm về kiến thức đạo hàm với phần lượng giác.
Hy vọng với những bài tập đạo hàm trên sẽ hữu ích cho các bạn. Mọi góp ý và thắc mắc các bạn vui lòng để lại bình luận dưới bài viết để daoham.com ghi nhận và hỗ trợ.