Bài tập tiếp tuyến liên quan tới đạo hàm

Đạo hàm có ứng dụng quan trong vào khảo sát hàm số, đặc biệt là bài tập tìm tiếp tuyến của hàm số. Dưới đây là những bài tập tiếp tuyến quan trọng

Bài 1: Cho hàm số y = cos $^2$ x + msinx (m là tham số) có đồ thị là (C). Tìm m trong mỗi trường hợp sau:

a. Tiếp tuyến của (C) tại điểm có hoành độ x = π có hệ số góc bằng 1.

b. Tiếp tuyến của (C) tại các điểm có các hoành độ x = – $\frac{\pi }{4}$ và x = $\frac{\pi }{3}$ song song hoặc trùng nhau.

Giải

Trước tiên, ta có: y’ = -2sinx.cosx + mcosx = -sin2x + mcosx.

a. Tiếp tuyến của (C) tại điểm có hoành độ x = π có hệ số góc bằng 1 điều kiện là:

y'(π) = 1 <=> -sin2π + mcosπ = 1 <=> m = -1.
với m = -1 thoả mãn điều kiện đầu bài.

b. Tiếp tuyến của (C) tại các điểm có các hoành độ x = – $\frac{\pi }{4}$ và x = $\frac{\pi }{3}$ có hệ số góc bằng:

k1 = y'(- 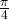$\frac{\pi }{4}$ ) = -sin(- 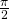$\frac{\pi }{2}$ ) + mcos(- 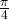$\frac{\pi }{4}$ ) = 1 + $\frac{{m\sqrt 2 }}{2}$ ,
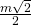k2 = y'( 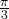$\frac{\pi }{3}$ ) = -sin 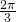$\frac{{2\pi }}{3}$ + mcos $\frac{\pi }{3}$ = – $\frac{{\sqrt 3 }}{2}$ + $\frac{m}{2}$ .

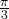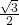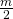Để hai tiếp tuyến song song hoặc trùng nhau điều kiện là:

k1 = k2 <=> 1 + $\frac{{m\sqrt 2 }}{2}$ = – $\frac{{\sqrt 3 }}{2}$ + $\frac{m}{2}$ <=> ( $\sqrt 2$ – 1)m = – $\sqrt 3$ – 1 <=> m = $\frac{{1 + \sqrt 3 }}{{1 - \sqrt 2 }}$ .

Vậy, với m = $\frac{{1 + \sqrt 3 }}{{1 - \sqrt 2 }}$ thoả mãn điều kiện đầu bài.

Bài 2:Cho Parabol (P): y = x $^2$ . Gọi M1 và M2 là hai điểm thuộc (P) lần lượt có hoành độ x1 = -2 và x2 = 1. Hãy tìm trên (P) một điển C sao cho tiếp tuyến tại C song song với cát tuyến M1M2. Viết phương trình tiếp tuyến đó.

Giải

Trước tiên, ta có: y’ = 2x.

Gọi k là hệ số góc của cát tuyến M1M2 với Parabol (P), ta có ngay: k = $\frac{{\Delta y}}{{\Delta x}}$

= $\frac{{f({x_1}) - f({x_2})}}{{{x_1} - {x_2}}}$ = $\frac{{{{( - 2)}^2} - {1^2}}}{{ - 2 - 1}}$ = -1.

M là điểm tuỳ ý thuộc đồ thị, giả sử M có hoành độ bằng a, khi đó:

Để tiếp tuyến tại M song song với cát tuyến M1M2 điều kiện là: y'(a) = -1 <=> 2a = -1 <=> a = – $\frac{1}{2}$ .
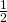Tại M(- 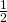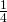$\frac{1}{2}$ ; $\frac{1}{4}$ ) phương trình tiếp tuyến có dạng: (d): y – 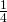$\frac{1}{4}$ = -(x + 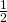$\frac{1}{2}$ ) <=> (d): y = -x – $\frac{1}{4}$ .

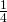Bài 3: Tìm giao điểm của hai đường cong (P): y = x $^2$ – x + 1 và (H): y = $\frac{1}{{x + 1}}$ . Chứng minh rằng hai đường cong đó có tiếp tuyến chung tại giao điểm của chúng.

Giải

Hoành dộ giao điểm là nghiệm của phương trình: x2 – x + 1 = $\frac{1}{{x + 1}}$

<=> $\frac{{{x^3}}}{{x + 1}}$ = 0=> x $^3$ = 0 <=> x = 0 => A(0; 1).

Vậy, hai đồ thị (P) và (H) cắt nhau tại điểm A(0; 1).

Ta lần lượt có:

Phương trình tiếp tuyến của (P) tại A có dạng: (d1): y – 1 = y’ 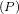$_{(P)}$ (0).x <=> (d1): y = -x + 1.
Phương trình tiếp tuyến của (H) tại A có dạng: (d2): y – 1 = y’ 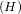$_{(H)}$ (0).x <=> (d2): y = -x + 1.

Nhận thấy (d1) ≡ (d2), tức là (P) và (H) có tiếp tuyến chung tại A.

Bài 4:Viết phương trình tiếp tuyến của đồ thị hàm số:

a. y = $\frac{{x - 1}}{{x + 1}}$ , biết hoành độ tiếp điểm là x $_0$ = 0.

b. y = $\sqrt {x + 2}$ , biết tung độ tiếp điểm là y $_0$ = 2.

Giải

a. Trước tiên, ta đi tính đạo hàm: y’ = $\frac{{x + 1 - (x - 1)}}{{{{(x + 1)}^2}}}$ = $\frac{2}{{{{(x + 1)}^2}}}$ .

Tại điểm có hoành độ x $_0$ = 0 phương trình tiếp tuyến có dạng: (d): y – y(0) = y'(0)(x – 0) <=> (d): y = 2x – 1.

b. Trước tiên, ta đi tính đạo hàm: y’ = $\frac{1}{{2\sqrt {x + 2} }}$ .

Tại điểm có tung độ y $_0$ = 2, ta lần lượt có:

Hoành độ tiếp điểm được cho bởi: 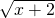$\sqrt {x + 2}$ = 2 <=> x + 2 = 4 <=> x = 2.
Phương trình tiếp tuyến có dạng: (d): y – y(2) = y'(2)(x – 2) <=> (d): y = 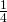$\frac{1}{4}$ x + $\frac{3}{2}$ .

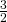Bài 5: Cho hàm số (C): y = x $^3$ – 3x $^2$ + 2. Viết phương trình tiếp tuyến của đồ thị, biết rằng tiếp tuyến vuông góc với đường thẳng (Δ): 3x – 5y – 4 = 0.

Giải

Ta có: y’ = 3x $^2$ – 6x và hệ số góc của đường thẳng (Δ) bằng $\frac{3}{5}$ .

Do đó, hoành độ tiếp điểm của tiếp tuyến với đồ thị hàm số là nghiệm của phương trình: y’. $\frac{3}{5}$ = – 1

<=> 3x $^2$ – 6x = – $\frac{5}{3}$

<=> 9x $^2$ – 18x + 5 = 0

<=> $\left[ \begin{array}{l}x = 1/3\\x = 5/3\end{array} \right.$ .

* Với x = $\frac{1}{3}$ , ta được tiếp tuyến (d1) có dạng: (d1): y = – $\frac{5}{3}$ (x – $\frac{1}{3}$ ) + y( $\frac{1}{3}$ )

<=> (d1): y = – $\frac{5}{3}$ x + $\frac{{61}}{{27}}$ .

* Với x = $\frac{5}{3}$ , ta được tiếp tuyến (d1) có dạng: (d2): y = – $\frac{5}{3}$ (x – $\frac{5}{3}$ ) + y( $\frac{5}{3}$ )

<=> (d2): y = – $\frac{5}{3}$ x – $\frac{{31}}{{27}}$ .

Vậy, tồn tại hai tiếp tuyến (d1), (d2) của đồ thị thoả mãn điều kiện đầu bài.

Bài 6: Viết phương trình tiếp tuyến của Parabol y = x $^2$ , biết rằng tiếp tuyến đó đi qua điểm A(0; -1).

Giải

Trước tiên, ta đi tính đạo hàm: y’ = 2x.

Giả sử hoành độ tiếp điểm là x $_0$ , khi đó phương trình tiếp tuyến có dạng:

(d): y – y(x $_0$ ) = y'(x $_0$ )(x – x $_0$ ) <=> (d): y – $x_0^2$ = 2x $_0$ (x – x $_0$ ). (*)

Vì điểm A(0; -1) ∈ (d) nên:

-1 – $x_0^2$ = 2x $_0$ (-x $_0$ ) <=> $x_0^2$ = 1 <=> x $_0$ = ±1.

Khi đó:

Với x $_0$ = 1, ta được tiếp tuyến có phương trình: (d1): y – 1 $^2$ = 2(x – 1) <=> (d1): y = 2x – 1.
Với x $_0$ = -1, ta được tiếp tuyến có phương trình: (d2): y – (-1) $^2$ = 2(-1)(x + 1) <=> (d2): y = -2x – 1.

Vậy, tồn tại hai tiếp tuyến thoả mãn điều kiện đầu bài.

admin

You might also like

Khái niệm về đạo hàm

Giá trị đạo hàm ${f^\prime }\left( 8 \right)$ bằng

Đạo hàm của hàm số y = cos(tanx) bằng