Cho hàm số ![]() . Đạo hàm y’ của hàm số là biểu thức nào sau đây?
. Đạo hàm y’ của hàm số là biểu thức nào sau đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Hướng dẫn giải
Đáp án C.
Ta có ![]() .
.
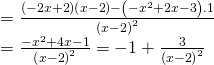 .
.
Hệ Thống Các Công Thức Đạo Hàm
Cho hàm số ![]() . Đạo hàm y’ của hàm số là biểu thức nào sau đây?
. Đạo hàm y’ của hàm số là biểu thức nào sau đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Hướng dẫn giải
Đáp án C.
Ta có ![]() .
.
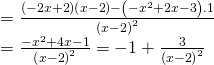 .
.