Đạo hàm u/v

I. Công thức đạo hàm phân thức u/v

Một hàm số phân thức có dạng $y = \frac{u}{v}$ thì khi tính đạo hàm:

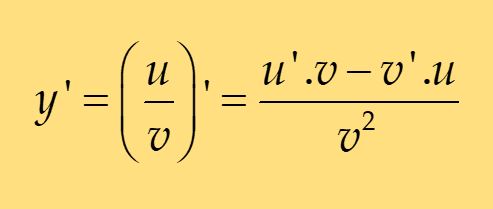
II. Bài tập minh họa

Bài tập 1: Hãy tính đạo hàm của hàm số sau: $y = \frac{1}{{2x}}$

Giải

Vận dụng công thức đạo hàm u/v ở trên: $y’ = \left( {\frac{1}{{2x}}} \right) = \frac{{\left( 1 \right)’.2x – \left( {2x} \right)’.1}}{{{{\left( {2x} \right)}^2}}} = – \frac{1}{{2{x^4}}}$

Bài tập 2: Cho một hàm phân thức có dạng $y = \frac{{{x^2} – 2x + 2}}{{x + 1}}$. Hãy tính đạo hàm của hàm này

Giải

Từ công thức của đạo hàm u/v trên, ta có:

$\begin{array}{l} y’ = \frac{{({x^2} – 2x + 2)'(x + 1) – ({x^2} – 2x + 2)(x + 1)’}}{{{{(x + 1)}^2}}}\\ = \frac{{(2x – 2)(x + 1) – ({x^2} – 2x + 2)}}{{{{(x + 1)}^2}}} = \frac{{{x^2} + 2x – 4}}{{{{\left( {x + 1} \right)}^2}}} \end{array}$

Bài tập 3: Cho hàm số có dạng $y = \frac{{2 – 2x + {x^2}}}{{{x^2} – 1}}$. Dựa vào đạo hàm phân thức u/v hãy giải.

Giải

Dựa vào công thức trên, ta có:

$y’ = \frac{{(2x – 2)({x^2} – 1) – 2x({x^2} – 2x + 2)}}{{{{({x^2} – 1)}^2}}} = \frac{{2{x^2} – 6x + 2}}{{{{({x^2} – 1)}^2}}}$

Bài tập 4: Cho hàm số lượng giác $y = \frac{x}{{\sin x}}$. Hãy tìm đạo hàm

Giải

Vận dụng công thức đạo hàm của hàm lượng giác: $y’ = \frac{{\sin x – x\cos x}}{{{{\sin }^2}x}}$

Bài tập 5: Sử dụng đạo hàm của hàm số lượng giác để tính $y = – \frac{{\cos x}}{{3{{\sin }^3}x}} + \frac{4}{3}\cot x$

Giải

Vận dụng công thức đạo hàm lượng giác:

$\begin{array}{l} y = – \frac{1}{3}\cot x(1 + {\cot ^2}x) + \frac{4}{3}\cot x = – \frac{1}{3}{\cot ^3}x + \cot x\\ y’ = {\cot ^2}x(1 + {\cot ^2}x) – 1 – {\cot ^2}x = {\cot ^4}x – 1 \end{array}$

.